CENTER OF GRAVITY
CONCEPT
It is a geometrical point located inside or outside of a body, through which passes the line of action of the resultant force of the gravity forces acting on each of the particles forming the body.
1. Weight (W) is a vector quantity. It is the resultant force exerted by the earth on the bodies around it. It is represented by a vector that indicates the center of the earth.
Weight = m.g
2. The center of gravity (G) is considered as the point where the weight of a body is concentrated, and on which a force numerically equal to the weight must be applied to establish the equilibrium.
3. When a body is held by different points, as shown in the figures, it is noted that the center of gravity is below the point of suspension.
If the suspension lines extend, we see that they intersect at the point where the center of gravity (G) of the body is.
4. With the Theorem of Varignon the center of gravity of the system with respect to a coordinate system is determined, for a body comprising constituents whose centers of gravity are set.
W = W1 + W2 + W3
5. The Theorem of Varignon with respect to the axis "y"
W.x = W1.x1+W2.x2+W3.x3
X: Abscissa of the center of gravity.
The Theorem of Varignon with respect to the axis "x"
W.y = W1.y1 + W2.y2 + W3.y3
Y: Ordinate of center of gravity.
6. For the bodies linearly homogeneous as in the figure above, the weight can be written in terms of its length.
The Weight is directly proportional to its length.
W1=K.L1 ; W2=K.L2 ; W3=K.L3
Replacing in equations (1) and (2), the following equations are obtained:
7. For the bodies superficially homogeneous (density constant and equal thickness), the weight is directly proportional to the area.
W1=K.A1 , W2=K.A2 , W3=K.A3
Substituting into equations (1) and (2).
8. For a system of bodies.
Weight = Specific weight x volume
W1=K.V1 , W2=K.V2 , W3=K.V3
Replacing values we obtain.
CENTER OF MASS
CONCEPT
It is the geometrical point where it is considered the concentration of the mass of a particle system.
When applying the Theorem of Varignon we can find the position of the mass center with respect to a coordinate system.
a) The position of the center of mass is defined by the coordinates (x, y)
b) Considering that weight = mg
c) These formulas can be generalized for a system "n" particles.
Therefore, in general terms:
Triangle
Given that the circumference is a plane curve and closed whose points are equidistant from another placed therein which is called the center and the circle is the area or plane surface that is contained within a circumference, then:
Illustrative exercises
1. The figure shows a cone of 40cm height and 20cm radius that it suspended from the point P.
If 0 is the midpoint of the base and P is the midpoint of the radius, determine the angle "θ" which forms the axis of the cone with the vertical.
Solution
In the equilibrium position, the weight (W) and the tension (T) are collinear, so the points P and G are in the same vertical.
OP is half the Radius, then OP = 10cm
2. In the vertex angles of a square of 2m side, four particles were placed. Determine the center of mass with respect to the coordinate system.
Solution
We have that the masses m1, m2, m3 and m4 weigh 1kg, 2kg, 3kg and 4kg respectively.
Then according to the position r = (X, Y) and considering the distance between particle and particle.
r1 = (0 ; 2)
r2 = (2 ; 2)
r3 = (2; 0)









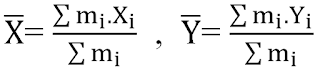


















No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.