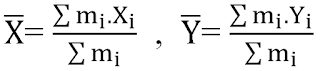SIMPLE HARMONIC MOTION

SIMPLE HARMONIC MOTION

CONCEPT

It is the oscillatory and periodic motion; it's made in a straight line caused by a restoring force, which is described mathematically by sine and cosine functions.

Restoring force (F)

It is the inner force that manifest the elastic bodies when they are stretched or compressed, acting on the particle "m" so that it recovers its equilibrium position.

The restoring force is the tension or compression of the springs, which is represented by a vector F acting on the particle, indicating the position of equilibrium.

Hooke's law:

K: Spring constant (N / M)

Elongation (X)

It is the magnitude of the vector and it indicates the position of the particle or body "m" in each instant of time "t" with respect to the equilibrium position.

Amplitude (A)

It is the maximum elongation reached by a moving particle.

The particle begins its movements (t = 0) when X = A and it is established that:

x (t) = A. Cos (ωt)

Relation between Simple Harmonic Motion and Uniform Circular Motion

If a particle moves with Uniform Circular Motion, then their projections on its diameter hold with the requirements of Simple Harmonic Motion.

Where X is the projection of the radius A on the horizontal axis.

The angle "θ" is the angular displacement experienced by the particle with a Uniform Circular Motion, θ = ω.t

X (t) = A Cos θ

X (t) = A Cos (ω.t)

PERIOD OF PARTICLE "m"

We analyze the particle mass "m" dynamically and perform the free body diagram at a given time "t".

 By Newton's second law:
 

FR=m.a

K.X = m(ω2.X)

K = m.ω2

We isolate ω and do the square root to both sides

Replacing values, we obtain

INSTANTANEOUS VELOCITY

It becomes the projection of the tangential velocity on the horizontal axis. The Velocity ​​(V) in the Uniform Circular Motion is V = ωA

V (t) = Vsenθ

V (t) = ωA.Sen (ωt)

INSTANTANEOUS ACCELERATION

It is the projection of the centripetal acceleration on the horizontal axis.

The centripetal acceleration in the Uniform Circular Motion is ω2.A

a(t) = ac . Cosθ

a(t) = ω2 . A. Cos(ωt)

Replacing values

a(t) = ω2 . X

ASSOCIATION OF SPRINGS

The springs tied to masses can be connected in two basic ways: in series and in parallel.

The set of springs may be replaced by a single equivalent spring whose spring constant is called equivalent spring constant (Ke)

SPRINGS IN SERIES

In the graph you can see that the tension that the springs are supporting is the same (T = KX)

In the case of equivalent displacement Xe, it is equal to the sum of the displacements of the each spring.

Xe = X1 + X2 + X3

* In the case of the association of springs in series:

SPRINGS IN PARALLEL

In all the springs the deformation X are the same.

The equivalent tension (Te) is represented by:

Te = T1 + T2 + T3

The tension on each spring is:

T1 = K1.X   ;   T2 = K2.X   ;    T3 = K3.X

→ Ke = K1 + K2 + K3

TOTAL ENERGY SYSTEM

A particle of mass "m" begins its movement at time t = 0, when the elongation is equal to the amplitude (x = A). The restoring force F acting on the particle "m" varies with the distance as shown in the graph.

 

The total energy of the mass-spring system is equal to the area under the line shown in the figure.

ETotal = Área

If:

ETotal = EC + Ep

Where V is the particle velocity in the instant in which "t" is the X distance from the equilibrium position.

THE SIMPLE PENDULUM

CONCEPT:

It is the system consisting of a mass "m" of a small size attached to a string and not extensible with negligible weight, which can oscillate around its equilibrium position, with a movement which is approximately the simple harmonic motion.

In order to identify the cause of oscillations, the free-body diagram of the pendulum mass "m" is performed. Thus, the restoring force is identified in a component of the weight (mg) which is tangent to the circumference.

F = m.g. Sin θ

It is known from the Second Law of Newton:

F = m.a

→ m.g.Sin θ = m.ω2.x

For small amplitudes it is established that (θ in radians)

x = θ.L = Sin θ.L

Replacing values:

g. Sinθ = ω2.Sinθ.L

Whereas:

Illustrative exercises:

1.- A box of mass "M" is on a horizontal table; plus the friction coefficient between the box and the table is equal to μ. Inside the box lies a body of mass "m" that can move without friction on the bottom of the box. This body is attached to the wall within the box as shown in the figure by a spring whose stiffness is K. With what amplitude of the oscillations of the body the box will begin to move on the table?

Solution

The maximum force F that the spring applies to the box is

F = K.A

When the spring is about to move, then the following situation states:

∑ Fx=0

F = fs(max)

F = µ. N;

But considering the system as a whole: N = (m + M) g

K.A. = µ(M+m)g

2.- The period of vibration of the system shown is 0.3 seconds. If block A is removed, the new period is 0.6 seconds. Knowing that the mass of the block A is 22,5 Kg, determine the mass of the block B. Consider that there is no friction.

Solution

It notes that the period of oscillation depends only on the system mass; and the stiffness constant depends on the material and shape of the spring.

- Whereas:

- The following case is also given:

 Dividing both results and simplifying values ​​we have:

Replacing mA=22,5Kg

CENTER OF GRAVITY AND CENTER OF MASS

CENTER OF GRAVITY

CONCEPT

It is a geometrical point located inside or outside of a body, through which passes the line of action of the resultant force of the gravity forces acting on each of the particles forming the body.

1. Weight (W) is a vector quantity. It is the resultant force exerted by the earth on the bodies around it. It is represented by a vector that indicates the center of the earth.

                                 Weight = m.g

2. The center of gravity (G) is considered as the point where the weight of a body is concentrated, and on which a force numerically equal to the weight must be applied to establish the equilibrium.

3. When a body is held by different points, as shown in the figures, it is noted that the center of gravity is below the point of suspension.

If the suspension lines extend, we see that they intersect at the point where the center of gravity (G) of the body is.

4. With the Theorem of Varignon the center of gravity of the system with respect to a coordinate system is determined, for a body comprising constituents whose centers of gravity are set.

W = W1 + W2 + W3

5. The Theorem of Varignon with respect to the axis "y"

W.x = W1.x1+W2.x2+W3.x3

 

X: Abscissa of the center of gravity.

The Theorem of Varignon with respect to the axis "x"

W.y = W1.y1 + W2.y2 + W3.y3

Y: Ordinate of center of gravity.

6. For the bodies linearly homogeneous as in the figure above, the weight can be written in terms of its length.

The Weight is directly proportional to its length.

W1=K.L1 ; W2=K.L2 ;  W3=K.L3

Replacing in equations (1) and (2), the following equations are obtained:

 

7. For the bodies superficially homogeneous  (density constant and equal thickness), the weight is directly proportional to the area.

W1=K.A1   , W2=K.A2  ,  W3=K.A3

Substituting into equations (1) and (2).

8. For a system of bodies.

Weight = Specific weight x volume

W1=K.V1 ,  W2=K.V2 ,   W3=K.V3  

Replacing values we obtain.

CENTER OF MASS

CONCEPT

It is the geometrical point where it is considered the concentration of the mass of a particle system.

When applying the Theorem of Varignon we can find the position of the mass center with respect to a coordinate system.

 

a) The position of the center of mass is defined by the coordinates (x, y)

b) Considering that  weight = mg

c) These formulas can be generalized for a system "n" particles.

Therefore, in general terms:

Triangle

Given that the circumference is a plane curve and closed whose points are equidistant from another placed therein which is called the center and the circle is the area or plane surface that is contained within a circumference, then:

Quarter Circumference

Semi Circumference

Quarter circle

Semicircle

Arc of Circumference

Sector of a Circle

Trapezium

Prism

Cylinder

Pyramid

Cone

Hemisfere

Illustrative exercises

1. The figure shows a cone of 40cm height and 20cm radius that it suspended from the point P.

  If 0 is the midpoint of the base and P is the midpoint of the radius, determine the angle "θ" which forms the axis of the cone with the vertical.

 Solution

In the equilibrium position, the weight (W) and the tension (T) are collinear, so the points P and G are in the same vertical.

OP is half the Radius, then OP = 10cm

 

2. In the vertex angles of a square of 2m side, four particles were placed. Determine the center of mass with respect to the coordinate system.

Solution

We have that the masses m1, m2, m3 and m4 weigh 1kg, 2kg, 3kg and 4kg respectively.

Then according to the position r = (X, Y) and considering the distance between particle and particle.

r1 = (0 ; 2)

r2 = (2 ; 2)

r3 = (2; 0)

r4 = (0 ; 0)